The term for what I needed was "Constructive solid geometry" or CSG.
CSG is the technique of creating complex objects from simple shapes such as spheres and cubes through boolean set operations such as difference, intersection and union.
It was at this point that I started off the beaten track. There was ample information on the concepts but very little in the way of concrete implementation which meant working a lot of this out myself.
So in an effort to smooth the way for those following me, grab a coffee and some snacks while I do my best to describe my approach as best as I can - it's going to be a long one.
The plan:
The approach is simple enough, these things often are - it is the implementation which is hard.Here are 2 meshes, mesh A which is a red cube and mesh B which is a blue sphere.
 |
| http://en.wikipedia.org/wiki/Constructive_solid_geometry |
I want to support the 3 main operations which are:
Difference: Subtract one meshes volume from the other, for example if mesh B was to subtract it's volume from mesh A, the algorithm must delete any portion of mesh A which lies inside of mesh B as well as deleting any portion of mesh B which does not lie inside of mesh A's volume.
Intersection: Return only the volume that both meshes share, any part of either mesh which does not lie inside the volume of the other mesh must be deleted.
Union: combine both meshes into one, deleteing any part of either mesh which lies inside of mesh A and mesh B.
To do this i will outline the general approach before going into detail.
1) Every polygon from either mesh which crosses inside the volume of the other mesh needs to be split along the intersection of the two meshes.
2) After splitting is complete all polygons should be classified as either inside or outside the volume of the other mesh and either kept or discarded depending on the operation.
To do this a data structure needs to be generated which represents the volume of the mesh in order to support classifying the polygons as inside or outside.
The data structure in use here is the "Binary space partition tree" (BSP tree) and revolves around classifying polygons as crossing a plane formed by another polygon or lieing to either side of that plane. A BSP tree will solve both step 1 and step 2.
I will go into detail and explain how to construct and use a BSP tree later, first I will describe how to classify a polygon to a plane and how to split a polygon against that plane which is a central concept used as part of constructing a BSP tree.
Classifying polygons:
 |
This means a way to describe which side of a plane a polygon lies on is required.
The code to calculate this can be simplified greatly by observing that triangles are by definition planar.
By splitting a triangle any polygons created as a result of that split must also be planar.
Because I am working with meshes entirely composed of triangles then only planar polygons need ever be considered.
Because of this, determining which side of a plane a polygon lies on is reduced to simply calculating the distance to the plane for all points in the polygon and testing if they are all are at a positive distance from the plane or at a negative distance from the plane.
DotProduct(point , PlaneNormal ) + D
where D is the dot product calculated between any of the points making up the polygon which the plane belongs to and the normal vector of the polygon being tested.
If the distance is positive or negative or 0 it can be classified as inside, outside or "on" the plane respectively.
A simple implementation:
//
public PointPlaneClassification ClassifyPointToPlane(Vertex Point)
{
double Distance = GetDistance(Point.Position);
if (IsEqual(Distance, 0.0, epsilon))
return PointPlaneClassification.Point_On_Plane;
if (IsGreaterThan(Distance, 0.0, epsilon))
return PointPlaneClassification.Point_Behind_Plane;
if (IsLessThan(Distance, 0.0, epsilon))
return PointPlaneClassification.Point_In_Front_Of_Plane;
return PointPlaneClassification.Point_On_Plane;
}
You might be wondering why I am using functions for the comparisons with 0 instead of the normal comparison operators - this is because CSG is an area where limited floating point precision is a really big problem. I recommend reading an introduction to managing finite floating point precision and how to work around it. (in this case by treating numbers within epsilon of 0 as 0).
It is then straight forward to extend this to be able to classify entire polygons.
//
public PolyIntersectType GetPolygonIntersectionType(Polygon polygon)
{
// short cut, if the two polygons are co-planar then only one point
// is required to know if the polygons coincident or disjoint on one side or the other.
double dot = Vector3Double.DotProduct(Normal, polygon.normal);
if (DoubleHelper.IsEqual(Math.Abs(dot), 1.0, DoubleHelper.epsilon))
{
for (int i = 0; i < polygon.Verticies.Length; i++)
{
PointPlaneClassification classification = ClassifyPointToPlane(polygon.Verticies[i]);
if (classification == PointPlaneClassification.Point_Behind_Plane)
return PolyIntersectType.DisjointPositive;
if (classification == PointPlaneClassification.Point_In_Front_Of_Plane)
return PolyIntersectType.DisjointNegative;
}
return PolyIntersectType.CoPlanar;
}
// not coplanar, test each point against the plane.
// if points exist on bothsides return Straddleing immediately.
int numFront = 0, numBack = 0;
for (int i = 0; i < polygon.Verticies.Length; i++)
{
PointPlaneClassification classification = ClassifyPointToPlane(polygon.Verticies[i]);
if (classification == PointPlaneClassification.Point_Behind_Plane)
numBack++;
if (classification == PointPlaneClassification.Point_In_Front_Of_Plane)
numFront++;
if (numFront != 0 && numBack != 0) return PolyIntersectType.Straddles;
}
// otherwise if all the points lie on the negative side, return disjoint negative.
if (numFront != 0) return PolyIntersectType.DisjointNegative;
// at this point the only possibility is that the polygon is disjoint on the positive side.
return PolyIntersectType.DisjointPositive;
}
Splitting polygons:
Now that it is possible to classify two polygons to a plane, it is time to describe how to split them by it.
Since it crosses the plane this is impossible, the triangle is both inside and outside of the plane at the same time.
Therefore in order to resolve this the triangle is split into two peices where it crosses the plane and one peice is classified as inside and the other as outside.
I had a go at it on my own and came up with an algorithm which walked around the edge of a polygon filling the vertex list of the first of 2 new polygons. The 2 new polygons represented the halves of the original polygon in the negative half space and the positive half space.
If an intersection was detected the intersection point was added to both polygon's vertex lists and the then the walking would continue except that it was the other polygon whose list was being filled.
Once the algorithm came back around and crossed the plane again once again the intersection point was added to both lists and the first polygon was once again the polygon whose list was being filled until the algorithm was back to the start.
This worked in the majority of cases, however, there was the odd edge case and handling them all was starting to become a pain so I decided to look around to if there was a better way.
Turns out I was pretty close, the overall concept was sound ,however, my approach was unnecessarily complicated.
One of my favourite references through this entire ordeal was "Real time collision detection" by Christer Ericson.
Basically, his approach was first of all to do away with filling one polygon, then the other and instead enumerate all the permutations that could happen when a vertex crossed a plane and insert verticies to either polygon depending on the combination of the current vertex and the next vertex being "On the plane" , "In front" or "Behind the plane". As a result the code came out much simpler and robust.
The final product was very similar to his example, for a thorough explanation I highly reccomend reading his book - it helped me immeasureably.
//
public Polygon[] SplitPolygon(Polygon polygon)
{
List<vertex> FrontVerticies = new List<vertex>(polygon.Verticies.Length + 1);
List<vertex> BackVerticies = new List<vertex>(polygon.Verticies.Length + 1);
Vertex A = polygon.Verticies[polygon.Verticies.Length-1];
PointPlaneClassification Aside = ClassifyPointToPlane(A);
for (int i = 0; i < polygon.Verticies.Length; i++)
{
Vertex B = polygon.Verticies[i];
PointPlaneClassification Bside = ClassifyPointToPlane(B);
switch (Bside)
{
case PointPlaneClassification.Point_In_Front_Of_Plane:
if (Aside == PointPlaneClassification.Point_Behind_Plane)
{
Vertex I = GetIntersection(B, A);
if (ClassifyPointToPlane(I) != PointPlaneClassification.Point_On_Plane) { }
FrontVerticies.Add(I);
BackVerticies.Add(I);
}
FrontVerticies.Add(B); // Output b to the front side
break;
case PointPlaneClassification.Point_Behind_Plane:
// Edge (a, b) straddles plane, output intersection point
if (Aside == PointPlaneClassification.Point_In_Front_Of_Plane)
{
Vertex I = GetIntersection(A, B);
if (ClassifyPointToPlane(I) != PointPlaneClassification.Point_On_Plane) { }
FrontVerticies.Add(I);
BackVerticies.Add(I);
}
else if (Aside == PointPlaneClassification.Point_On_Plane)
{ // Output a when edge (a, b) goes from ‘on’ to ‘behind’ plane
BackVerticies.Add(A);
}
// In all three cases, output b to the back side
BackVerticies.Add(B);
break;
case PointPlaneClassification.Point_On_Plane:
FrontVerticies.Add(B);
BackVerticies.Add(B);
break;
}
A = B;
Aside = Bside;
}
Polygon[] returnPolygons = new Polygon[2];
if (BackVerticies.Count > 2)
returnPolygons[0] = new Polygon(BackVerticies.ToArray(), polygon.Id , polygon.FlipNormals , polygon.normal);
if (FrontVerticies.Count > 2)
returnPolygons[1] = new Polygon(FrontVerticies.ToArray(), polygon.Id, polygon.FlipNormals, polygon.normal);
return returnPolygons;
}
You might be wondering why the polygon object has a "Id" and "FlipNormals" field - this all becomes important in the next section.
Binary space partition trees:
Bringing all these concepts together is the BSP tree.It is all well and good to be able to decide if two polygons are intersecting and to have a way to split them, but it is not much use without the ability to determine if a given polygon lies inside a meshes volume.This is required so that a particular polygon can be kept or discarded as required.
A data structure which provides what is needed is the "Binary Space Partition" (BSP) tree.
I'm going to demonstrate how they work as a 2d diagram, to generalize into 3d space imagine that each line in the polygon is a triangle. The theory works exactly the same.
Each edge in this polygon is given a letter and has a normal vector indicated by a short line pointing out from the center of the edge, this points the way to the "outside" or "empty space".
I will refer to this polygon below simply as "the polygon"
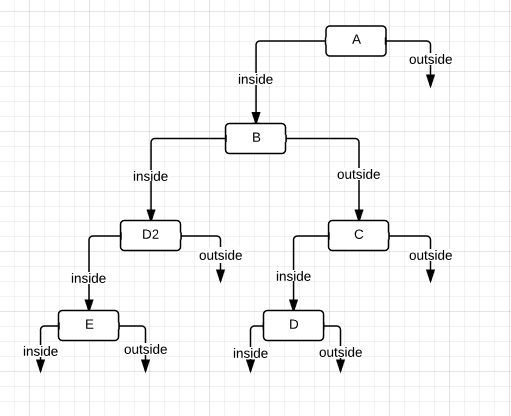
The way a BSP tree is built is one edge at a time. Each time an edge is added it's plane is used to further divide the world into two equal halves, the inside half and the outside half.
I'm going to start with edge A and work through alphabetically.
Below is A's plane Indicated in red - demonstrating how it splits space into 2 halves, the upper half (outside) and the lower half (inside).
It is possible to be inside A's plane and outside of the polygon as a whole at the same time.
Now to add the next edge "B". Always start from the top of the tree.
Is this edge on the inside of A's plane? Or on the outside?
Since the outside is the side which the normal is pointing and since B lies on the opposite side, B is therefore on the "Inside" half of A's plane.
So B is inserted into the tree at A's inside node.
And the graphics representation:
The next step is to add C.
The process is the same, is C inside or outside of A?
C is inside.
Therefore the "inside" half of the tree is tested next.
Is C inside or outside of B?
C is outside.
Therefore C is inserted into the tree on B's outside.
Now it gets a little more tricky.
Edge D needs to be inserted, So begin at A as usual.
Is D inside or outside of A?
D is inside, So B is tested against next.
Is D inside or outside of B?
Trick question? D crosses over B, it is both inside and outside.
The solution is to split D into two halves and send each half down the appropriate side.
I'll name the inside half D2 to differentiate it from D which will go down the outside half.
D will then be tested against C, where it lies on the inside half and is added to the tree.
D2 is simply added to B's inside half.
And then last of all E.
E is inside A.
E is inside of B
E is inside of D2, so it is added to the tree on D2's inside half.
And there is the completed BSP tree!
The code:
I'll outline an example here of how this might work.First some enums to describe the types of intersections.
enum PolyIntersectType
{
DisjointPositive,
DisjointNegative,
CoPlanar,
Straddles,
}
The bsp tree:
class BspTree
{
Plane DividingPlane;
BspTree PositiveHalf;
BspTree NegativeHalf;
private BspTree(Polygon P)
{
DividingPlane = new Plane(P);
}
public static BspTree ConstructTree(List<Polygon> PolygonList)
{
BspTree root = new BspTree(PolygonList[0]);
for (int i = 1; i < PolygonList.Count; i++)
{
root.PartitionPolygon(PolygonList[i]);
}
return root;
}
public bool PolygonLiesInsideVolume(Polygon P)
{
PolyIntersectType Type = DividingPlane.GetPolygonIntersectionType(P);
switch (Type)
{
// to stop c# complaining about not all code paths returning a value.
default: throw new ArgumentOutOfRangeException();
case PolyIntersectType.DisjointNegative:
// if at leaf node polygon is in empty space.
if (NegativeHalf == null) return false;
// test negative half, return the result.
return NegativeHalf.PolygonLiesInsideVolume(P);
case PolyIntersectType.DisjointPositive:
// if at leaf node - polygon is in solid space.
if (PositiveHalf == null) return true;
// test positive half, return the result.
return PositiveHalf.PolygonLiesInsideVolume(P);
case PolyIntersectType.Straddles:
// partition polygon by plane.
Polygon[] Splits = DividingPlane.SplitPolygonByPlane(P);
bool negHalf = false; bool posHalf = false;
if (PositiveHalf != null && Splits[0] != null) posHalf = PositiveHalf.PolygonLiesInsideVolume(Splits[0]);
if (NegativeHalf != null && Splits[1] != null) negHalf = NegativeHalf.PolygonLiesInsideVolume(Splits[1]);
// if at a leaf node, if either half of the polygon is discovered
// to be inside the volume return true.
if (negHalf && PositiveHalf == null && Splits[0] != null) return true;
if (posHalf && NegativeHalf == null && Splits[1] != null) return true;
// return true if either halves are in solid space.
return negHalf && posHalf;
case PolyIntersectType.CoPlanar:
return false;
}
}
private void PartitionPolygon(Polygon P)
{
PolyIntersectType Type = DividingPlane.GetPolygonIntersectionType(P);
switch (Type)
{
case PolyIntersectType.DisjointNegative:
// partition to negative half space.
DividingPlane.GetPolygonIntersectionType(P);
PartitionToNegativeHalf(P);
break;
case PolyIntersectType.DisjointPositive:
// partition to positive half space.
PartitionToPositiveHalf(P);
break;
case PolyIntersectType.Straddles:
// split polygon and partition to both sides.
Polygon[] Splits = DividingPlane.SplitPolygonByPlane(P);
if (Splits[0] != null) PartitionToPositiveHalf(Splits[0]);
if (Splits[1] != null) PartitionToNegativeHalf(Splits[1]);
break;
case PolyIntersectType.CoPlanar:
// polygon shares the same plane as this node.
// no need to partition at all.
break;
}
}
private void PartitionToNegativeHalf(Polygon P)
{
// if the positive half has not been used yet - create it.
if (NegativeHalf == null)
{
NegativeHalf = new BspTree(P);
}
else // otherwise partition polygon to positive half.
{
NegativeHalf.PartitionPolygon(P);
}
}
private void PartitionToPositiveHalf(Polygon P)
{
// if the positive half has not been used yet - create it.
if (PositiveHalf == null)
{
PositiveHalf = new BspTree(P);
}
else // otherwise partition polygon to positive half.
{
PositiveHalf.PartitionPolygon(P);
}
}
}
Putting BSP trees to use: point in mesh test.
BSP trees are useful for a couple of reasons, the first is that they provide a really effective way of determining if a point is inside a mesh and secondly they as a side effect of the method of construction create all the splits we need to perform CSG on two meshes.First I'll demonstrate how to use a BSP tree to decide if a point lies inside the mesh or not, it is a similar process to construction - just drop the point through the tree.
Putting them to use 2: Constructive solid geometry.
The main purpose of using BSP trees, however, is that because splitting polygons is a part of constructing them, merging two BSP trees created from two separate meshes will result in splits in all the places needed to perform any CSG operation, by keeping a copy of the original BSP trees from the mesh they can be used as demonstrated above to classify the polygons which were split as either inside or outside and then discard or keep them as required. First off I am going to overlay a new triangle with sides X Y Z. What I want to do is subtract this triangle from the first polygon so that it cuts a little triangle shaped hole - this is a "difference" operation.
What needs to be done next is to take a copy of the polygon's BSP tree so that it can be merged with the triangle's BSP tree and still be able to use the original to classify polygons as inside or outside at the end.
Each edge of the triangle is inserted into the copy of the polygon's BSP tree one edge at a time just like before with one twist; if an edge from the triangle crosses an edge from the polygon it needs to be split just as normal but - it also must split the edge from the polygon that it crossed.
( This is only strictly required if the polygons, not their planes are intersecting - see optimisation 2 below.)
Edge X from the triangle is inserted first, X crosses edge A.
X is split the two halves are passed down both the inside and outside of A as normal.
However because A was crossed by X it also needs to be split - but it doesnt need to be partitioned. It is stored in the same node (A , A2)
Y is partitioned cleanly down the tree until edge E.
Y is split into two halves and passed down both sides, E is also split just as A was.
Z is able to be partitioned as normal since it doesnt intersect with anything, It is split by A but A is not split by Z.
Remember before when I commented on polygons having an "ID" member? Now that the two meshes polygons are all mixed up together it is important to be able to tell them apart in order to be able to separate them again later.
If you look at the last diagram you can see that all the splits that need to be made in order to cut a hole into the polygon have already been made - now all that remains is to decide which polygons need to be thrown out.
The way I did this was to start at the top of the tree and work my way down copying all the polygons from each mesh into separate lists. Once I had all the polygons I then, one at a time, tested them against the original BSP from the other mesh in order to determine if they lay inside or outside of the mesh's volume.
In order to create a triangle shaped hole, all the triangle edges that are located outside of the polygon are discarded and all of the polygon edges that are located inside of the triangle also need to be discarded.
I'll leave the implementation of that to the reader, The result is this:
Improving performance:
My initial tests showed satisfactory performance when I intersected 2 small cubes together however once the size of the mesh was increased to what I expected to use in the game, the process just took too long and would cause frame rate skips. The only way to improve performance in a program is to reduce the amount of work the computer needs to do - by either working smarter or reducing the size of the problem.Optimisation 1: bounding boxes.
The first optimisation came about from realising that the only polygons which could be inside the other mesh or involved in an intersection must pass inside the the intersection of the two meshes bounding boxes. All other polygons could either be thrown out or kept depending on what the operation was right from the beginning.
The edges highlighted in red are the only edges which need to be included in the bsp tree - all the others are automatically classed as "outside".
So in the above example where I wanted to cut a triangle shaped hole, this means edge A, B,C,D can immediately be put in the keep list, edge Z can be immediately discarded without any further processing.
This can result in massive performance gains when the meshes involved are composed of thousands of polygons. For my purposes, where the player would be making edits on the scale of 1 small block and because the size of the terrain was so big, the bounding box intersection only covered a handful of polygons from the terrain. This reduced the number of polygons involved massively and resulted in a big framerate improvement.
It is possible to eliminate even more polygons quickly by using the solid leaf BSP trees that were built before the merge to perform some extra culling.
The key is in realising that partitioning polygons is really quite a lightweight operation compared to splitting them. Before creating the final merged BSP tree out of all the polygons which survived the bounding box intersection test, each list of polygons is dropped through the other mesh's BSP tree.
If a polygon is classified as either clearly inside or outside - then that polygon can be discarded or kept as required right there and then. If it crosses a plane then return it back into the list to build the final merged BSP tree with.
Optimisation 2: To split or not to split.
The final tweak which I used came about from observing the possibility of two polygons to be aligned such that the plane of one polygon will cause a split in the second polygon even though the two polygons are not actually touching. So when a polygon P from mesh A is being inserted into mesh B's bsp tree, P is split and partitioned just as normal - however the polygons in mesh B only need to be split as well if P is physically touching them. It is entirely correct to go ahead and split those polygons in B anyway - but a much higher mesh quality and increased performance can be gained by first running a strict polygon - polygon intersection test before deciding if to split or not.
No optimisation.
You can see how on the left, the result is absolutely valid - but there are massive amounts of unnecessary splits as showing in the wireframe on the right.
With optimisation:
The result is still just as valid but as shown on the wireframe on the right this mesh is much better. This runs much faster because all those extra polygons don't need to be processed.
No comments:
Post a Comment